Sainik School Class 6 LCM and HCF

Understanding LCM and HCF: Essential Rules for Sainik School Class 6 Entrance Exam

The Sainik School entrance exam (AISSEE) is a challenging test that requires a strong foundation in various mathematical concepts. Among these, the concepts of Least Common Multiple (LCM) and Highest Common Factor (HCF) are crucial for Class 6 students. These topics not only appear frequently in exams but are also fundamental for understanding more advanced mathematics. Mastering LCM and HCF can help students solve a wide range of problems with confidence and accuracy. In this post, we discuss the Sainik School Class 6 LCM and HCF, a very important topic for students for the Sainik School entrance exams.

What is LCM (Least Common Multiple)?

The Least Common Multiple (LCM) of two or more numbers is the smallest multiple that is common to all the numbers. In simpler terms, it’s the smallest number that each of the given numbers can divide without leaving a remainder.

How to Find the LCM

There are a few methods to find the LCM of two or more numbers:

Listing Multiples:
- List the multiples of each number until you find the smallest common multiple.

Example: Find the LCM of 4 and 6.

- Multiples of 4: 4, 8, 12, 16, 20, 24, …
- Multiples of 6: 6, 12, 18, 24, …
- The LCM of 4 and 6 is 12.
Prime Factorization:
- Break each number down into its prime factors, then multiply the highest powers of all prime factors together.

For example: Find the LCM of 8 and 12.

- Prime factorization of 8: 232^323
- Prime factorization of 12: 22×312^2 \times 3^122×31
- LCM = 23×31=242^3 \times 3^1 = 2423×31=24.
Division Method:
- Divide the numbers by common prime factors until you reach 1 for all numbers, then multiply the divisors.

Example: Find the LCM of 10, 15, and 20.

- Divide by 2: 10÷2=510 \div 2 = 510÷2=5, 15÷2=1515 \div 2 = 1515÷2=15, 20÷2=1020 \div 2 = 1020÷2=10
- Divide by 3: 555, 15÷3=515 \div 3 = 515÷3=5, 101010
- Divide by 5: 5÷5=15 \div 5 = 15÷5=1, 5÷5=15 \div 5 = 15÷5=1, 10÷5=210 \div 5 = 210÷5=2
- Divide by 2: 111, 111, 2÷2=12 \div 2 = 12÷2=1
- LCM = 2×3×5×2=602 \times 3 \times 5 \times 2 = 602×3×5×2=60.

What is HCF (Highest Common Factor)?

The Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), is the largest factor that divides two or more numbers without leaving a remainder. The HCF is useful in simplifying fractions and solving problems related to divisibility.

How to Find the HCF

There are several methods to find the HCF of two or more numbers:

Listing Factors:
- List all factors of each number and find the largest common factor.

Example: Find the HCF of 18 and 24.

- Factors of 18: 1, 2, 3, 6, 9, 18
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- The HCF of 18 and 24 is 6.
Prime Factorization:
- Break each number down into its prime factors, then find the common prime factors and multiply them together.

For example: Find the HCF of 28 and 42.

- Prime factorization of 28: = 2 × 2 × 7
- Prime factorization of 42: 2 × 3 × 7
- HCF = 2 $\times$ 7 = 14.
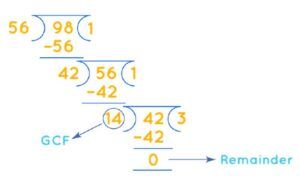
Division Method:
- Divide the larger number by the smaller number, then divide the remainder by the previous divisor. Repeat this process until the remainder is 0. The last divisor is the HCF.

Example: Find the HCF of 56 and 98.

- HCF = 14.

Importance of LCM and HCF in the AISSEE

LCM and HCF are essential concepts that are tested in the AISSEE for Class 6. These topics are foundational for solving a wide range of mathematical problems, including those involving fractions, ratios, and proportions. Understanding how to calculate LCM and HCF is crucial for performing well in the Maths section of the entrance exam.

Types of Problems Involving LCM and HCF

Word Problems:
- Problems that require finding the LCM or HCF to solve real-life scenarios, such as determining the least number of items needed for equal distribution or finding the maximum length of rods that can be cut evenly.

Example: Two bells ring at intervals of 4 and 6 minutes. After how many minutes will they ring together again?

- Solution: Find the LCM of 4 and 6, which is 12. The bells will ring together after 12 minutes.
Simplifying Fractions:
- Using the HCF to simplify fractions to their lowest terms.

Example: Simplify the fraction 42/56

- Solution: The HCF of 42 and 56 is 14. So, 42/56=3/4
Finding Common Multiples and Divisors:
- Problems that require finding the common multiples or divisors of numbers, often using LCM or HCF.

Example: Find the smallest number that is divisible by both 8 and 12.

- Solution: The LCM of 8 and 12 is 24, so the smallest number divisible by both is 24.

Tips for Mastering LCM and HCF

Practice Different Methods:
- Familiarize yourself with all methods for finding LCM and HCF, so you can choose the most efficient one for each problem.
Work on Word Problems:
- Practice solving word problems that require the use of LCM and HCF. This will help you apply these concepts to real-life situations.
Understand Prime Factorization:
- Prime factorization is a powerful tool for finding both LCM and HCF. Ensure you understand how to break numbers down into their prime factors.
Check Your Work:
- Always double-check your calculations, especially when working with large numbers or multiple steps.

Common Mistakes to Avoid

Confusing LCM and HCF:
- Remember that LCM is about finding the smallest common multiple, while HCF is about finding the largest common factor.
Incorrect Prime Factorization:
- Ensure you correctly factorize numbers into their prime components. A mistake here can lead to incorrect LCM or HCF values.
Forgetting to Simplify:
- After finding the HCF, always simplify fractions fully to ensure your answer is in the simplest form.
Overlooking Multiples and Factors:
- When listing multiples or factors, be thorough to avoid missing the correct LCM or HCF.

Conclusion

LCM and HCF are critical topics in the Sainik School Class 6 entrance exam’s Maths section. By mastering these concepts, students can solve a wide range of mathematical problems with confidence. Regular practice, a strong understanding of prime factorization, and the ability to apply these concepts to real-life scenarios will help students excel in the AISSEE and build a solid foundation for future mathematical studies.

Important Questions Related to Sainik School Class 6 LCM and HCF

Ques 1: Find the HCF of 160, 165, and 305.

a) 4

b) 5

c) 3

d) 6

Answer – b (5)

160 = 2 × 2 × 2 × 2 × 2 × 5
165 = 3 × 5 × 11
305 = 5 × 61
HCF= 5

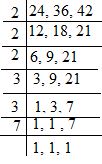
Ques 2: Find the LCM of 24, 36 and 42.

a) 504

b) 144

c) 196

d) 256

Answer – b (504)

LCM = 2 × 2 × 2 × 3 × 3 × 7 = 504

Ques 3: Find the maximum number of students among whom 429 mangoes and 715 oranges can be equally distributed.

a) 23

b) 69

c) 129

d) 143

Answer – d (143)

Solution:

429 = 3 × 11 × 13
715 = 5 × 11 × 13
HCF of 429 and 715= 11 × 13= 143

Ques 4: Find the least number which is divided by 12, 15, 20, and 25 exactly.

a) 500

b) 200

c) 300

d) 400

Answer – c (300)

LCM of 12, 15, 20, 25 = 300. Hence the least number which is exactly divided by 12, 15, 20, and 25 is 300.

For more such questions on Sainik School Class 6 LCM and HCF, download Shaurya Bharat app now: https://play.google.com/store/apps/details?id=com.shauryabharat

How to crack the AISSEE 2025 and RMS CET 2024 examinations?

Entrance examinations for Rashtriya Military School and Sainik School will take place in December 2024 and January 2025 respectively for academic session 2025-26. The best idea to start preparation is to start early so that students get sufficient time to prepare and polish themselves. The Sainik School and RMS Entrance Exams are a tough nut to crack. The standards and competition are way higher than one could think. Getting admission into Sainik School and RMS is the dream of thousands of young children. However, only a few can turn this dream into reality.

To succeed in this competitive environment, candidates need to prepare thoroughly, maintain a disciplined study routine, and focus on developing a strong foundation in the relevant subjects. Regular practice, solving sample papers, and mock tests can help in building confidence and improving performance. Maintaining physical fitness and participating in extracurricular activities can enhance overall candidacy.

It is important to remember that the competition is tough. However, dedication, hard work, and a positive mindset can significantly increase your chances of securing admission to a Sainik School or RMS. Here, Shaurya Bharat can be a perfect guide to students. Shaurya Bharat is the best offline and online platform for students preparing for the Sainik School, RMS, and RIMC entrance examinations.

Offline Classes

We conduct offline coaching for Sainik School and RMS (School + Coaching) at our campus in Jodhpur, Rajasthan.

Click the following link to get a virtual tour of Shaurya Bharat Sainik School and Defence Academy. https://www.youtube.com/watch?v=H1dDOpZ-kh8

Click the following link to get to know what students say about Shaurya Bharat Sainik School & Defence Academy https://www.youtube.com/watch?v=aYtCzAcU8To

Online Classes

Online classes are conducted through the Shaurya Bharat app. The Shaurya Bharat app provides the best content in the form of live classes, video lectures, and e-books.

Also, it offers topic-wise practice tests and pattern-based live exams. The live exams are based exactly on the pattern of the main examination. This gives students a well-required practice and a look and feel of the main examination. It makes them well-equipped to handle and overcome the examination pressure with minimum ease.

Useful Links

To know more about the Shaurya Bharat app logon to https://shauryabharat.com/

For more information about the Sainik School and RMS entrance exams for class 6, log on to https://shauryabharat.com/elite-schools/aissee-sainik-school-class-6/ and https://shauryabharat.com/elite-schools/rashtriya-military-school-rms-class-6/

For more information about the Sainik School and RMS entrance exam for class 9, log on to https://shauryabharat.com/elite-schools/aissee-sainik-school-class-9/ and https://shauryabharat.com/elite-schools/rashtriya-military-school-rms-class-9/

To download the detailed notification, submit the online application and download the admit card log on to https://exams.nta.ac.in/AISSEE/and https://www.rashtriyamilitaryschools.edu.in/

Use the following link to download the Shaurya Bharat app – The best digital platform to prepare for the Sainik School: https://play.google.com/store/apps/details?id=com.shauryabharat